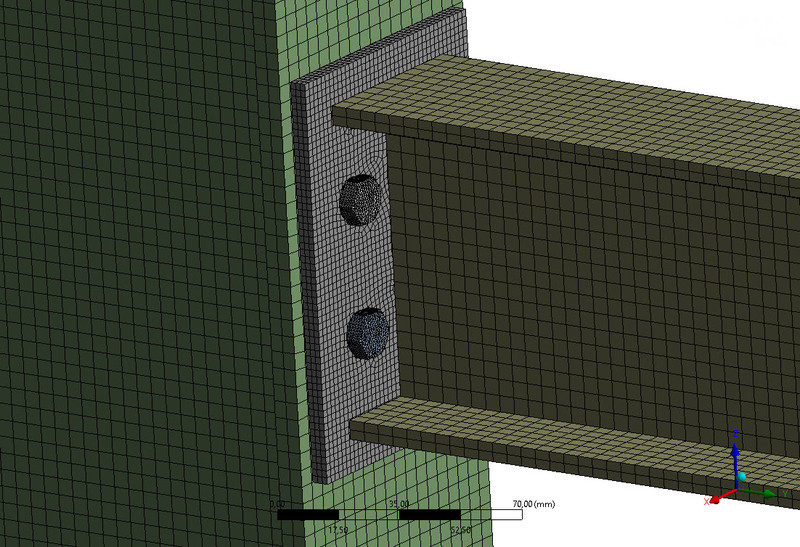
The Finite Element Method (FEM), also called "Method of finite elements", is a numerical method to solve partial differential equations. This method is a modern calculation method and widely used in engineering. The method provides an approximate function to the exact solution of the differential equation. The accuracy of the calculations can be improved by increasing the degrees of freedom. At the same time, however, this also increases the computational effort.
The FEM analyses can be used to work on a variety of engineering tasks. The different types of analysis include, for example, the following:
- Linearity/non-linearty static calculations
- Linearity/non-linearty static calculations
- Temperature field calculations
- Dynamic response in the time and frequency domains
- Earth quake simulations
- Rotor dynamic
- Stability analysis
- Flow simulation
- Fatigue life analysis
- Topology optimization