Finite Element Berechnungen

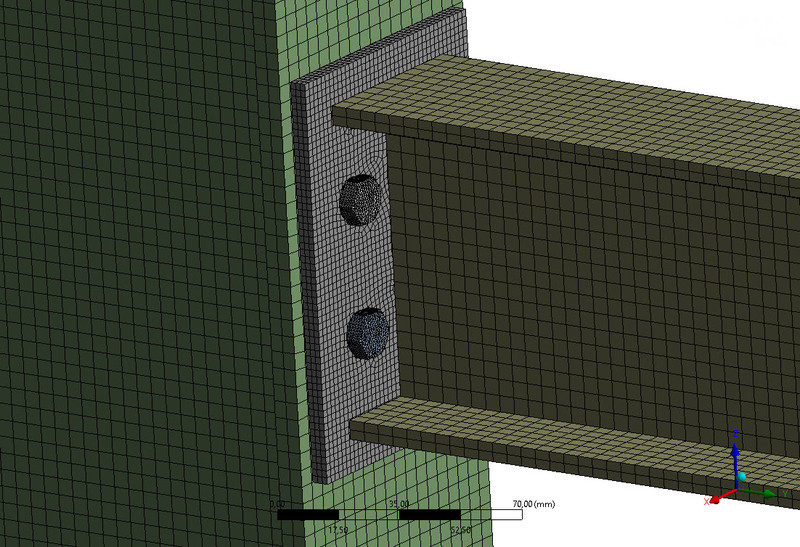
Die Finite-Elemente-Methode (FEM), auch „Methode der finiten Elemente“ genannt, ist ein numerisches Verfahren mit dem partielle Differentialgleichungen gelöst werden. Diese Methode ist ein modernes Berechnungsverfahren und weit verbreitet im Ingenieurswesen. Das Verfahren liefert eine Näherungsfunktion an die exakte Lösung der Differentialgleichung. Die Genauigkeit der Berechnungen kann durch die Erhöhung der Freiheitsgrade verbessert werden. Gleichzeitig steigt damit aber auch der Rechenaufwand.

Die FEM Analysen können dazu verwendet werden eine Vielzahl von ingenieurstechnischen Aufgabenstellungen zu bearbeiten. Zu den unterschiedlichen Analysearten zählen beispielsweise:

Lineare/nichtlineare Statik
Eigenwertprobleme (Eigenfrequenzen, Modalanalysen)
Temperaturfeldberechnungen
Dynamisches Antwortverhalten im Zeit- und Frequenzbereich
Erdbebensimulationen
Rotordynamik
Stabilitätsuntersuchungen
Strömungssimulation
Lebensdaueranalysen
Topologieoptimierung

Vom CAD- zum FE-Modell

Für das zu untersuchende Bauteil wird ein 3D CAD-Modell angefertigt, das exakt die geometrischen Verhältnisse beschreibt. Für bestimmte geometrische Details werden ggfs. Vereinfachungen vorgenommen, z.B. unwichtige Details wie etwa Bohrungen, Fasen oder Schweißnähte nicht mit modelliert. Diese Schritte werden als Idealisierung bezeichnet.

Im Bauwesen kommt es öfters dazu, dass einige Bauteile eine Symmetrie aufweisen und so eine Reduzierung des Berechnungsmodells zulassen. Durch das Verwenden von Symmetrierandbedingungen können so die gleichen Aussagen getroffen werden, wie für ein Vollmodell. Durch kleinere Modelle werden die Rechenzeiten verkürzt und die zu verarbeitenden Datenmengen verringert.

Berechnung / FEM Analyse

Bevor die eigentliche Berechnung durchgeführt werden kann, müssen die Lasten und Randbedingungen (Lagerung, Materialeigenschaften, etc.) festgelegt werden. Danach wird das Modell an den Solver übergeben, der zunächst eine Plausibilitätskontrolle durchführt und prüft, ob genügend Randbedingungen formuliert wurden, um das Problem zu lösen. Ist dies nicht der Fall, wenn z.B. Elemente ein zu stark verzerrtes Netz aufweisen oder die zu berechnenden Körper verschieblich sind, wird die Analyse abgebrochen.

Sofern die Randbedingungen vollständig definiert sind, wird das physikalische Modell in ein mathematisches umgewandelt. Dazu werden Steifigkeitsmatrizen erstellt, welche die Eigenschaften des Modells wiedergeben. Zusammen mit den einwirkenden Lasten ergibt sich ein Gleichungssystem, das der Solver zu lösen versucht. Die Ergebnisse können in unterschiedlichen Größen dargestellt werden: